There’s nothing quite like a maddening math problem, mind-bending optical illusion, or twisty logic puzzle to halt all productivity in the office. We’re curious people by nature, but we also collectively share a stubborn insistence that we’re right, dammit, and so we tend to throw work by the wayside whenever we come upon a problem with several seemingly possible solutions.
This triangle brain teaser isn’t new—shoutout to Popsugar for unearthing it a couple years ago—but based on some shady Internet magic, the tweet below reappeared in my feed today and kick-started a new debate on our staff-wide Slack channel, a place traditionally reserved for workshopping ideas, but instead mostly used for yelling about other stuff that we occasionally turn into content.
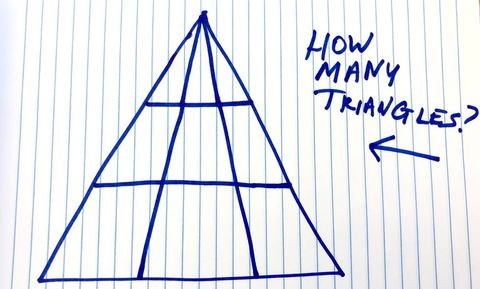
Because I’m a masochist, I drew the triangle again and asked everyone on staff to promptly drop what they were doing and attempt to solve the simple question: How many triangles can you find?
I’ll spare you the full conversation—trust me, nobody wants to see that—but the team’s responses ranged all over the place. Some editors saw four triangles. Others saw 12. A few saw 6, 16, 22. Even more saw 18. One wiseguy counted the triangles in the A’s in the question itself, while another seemed to be having an existential crisis: “None of these lines are truly straight, just curves—thus you cannot define any of them as a triangle,” he said. “There are no triangles in this photo. Life has no meaning.”
We then posed the problem to our Instagram followers, whose replies also ran the gamut, from 5 to 14 to 37. While we acknowledge the high probability of trolling here, it’s clear that people respond to the problem many different ways.
I could’ve listened to my colleagues explain their questionable processes all day, but instead, I reached out to several geometry experts to see if we could arrive at a consensus answer. Turns out virtually all of the mathematicians I contacted found the same solution—but not all of them figured it out in the same way.
If you don’t want to know the answer just yet, stop reading and try to solve the problem first. I’ll meet you back here when you’re done.
Hey, that was quick. Ready for the answer? Unlike some viral math problems that are purposely vague and open for interpretation, this one actually does have a slam-dunk, no-doubt-about-it solution, and it’s 18. Let’s hear from some of the geometry experts as to why.
“I would approach this just like one approaches any mathematical problem: reduce it and find structure,” says Sylvester Eriksson-Bique, Ph.D., a postdoctoral fellow with the University of California Los Angeles’s math department.
The only way to form triangles in the figure I drew, Erikkson-Bisque says, is if the top vertex (corner) is part of the triangle. The base of the triangle will then have to be one of the three levels below. “There are three levels, and on each you can choose a base among six different ways. This gives 18, or 3 times 6 triangles.”
Let’s look at the master triangle again.
“It’s convenient to generalize to the case where there are n lines passing through the top vertex, and p horizontal lines,” says Francis Bonahon, Ph.D., a professor of mathematics at the University of Southern California.
In our case, n = 4, and p = 3. Any triangle we find in the drawing should have one top vertex and two others on the same horizontal line, so for each horizontal line, the number of triangles with two vertices on that line is equal to the number of ways we can choose these vertices, Bonahon says—namely the number of ways we can choose two distinct points out of n, or “n choose 2.”
Remember high school math? That’s n(n-1)/2. And since there are p horizontal lines, says Bonahan, this gives p n(n-1)/2 possible triangles. In our case, that’s 3×4(4-1)/ 2=18.
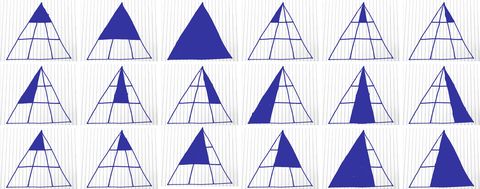
Here’s a handy breakdown of how to find each possible triangle:
Johanna Mangahas, Ph.D., an assistant math professor at the University at Buffalo, also came to 18—first through simple brute-force counting, then through the same crafty combinatorics as above—but admits our triangle brain teaser isn’t quite as cool as this one from Po-Shen Loh, Ph.D., a math professor at Carnegie Mellon University in Pittsburgh, as featured in the New York Times last year:
This one has a slicker mathematical answer, she says, because here, counting triangles is the same thing as counting combinations of three lines chosen out of six [6-choose-3 = (6*5*4)/(3*2*1)].
“In that case, every pair of lines intersects and there are no triple-or-more intersections, so any choice of three always gives a triangle,” says Mangahas. In the picture I sent her, some lines are parallel, so they can’t be part of the same triangle. “If you took the same seven lines and shook them up a bit, probabilistically they’d most likely land like [Loh’s] problem and you’d have more triangles and a similar cute answer.” (For the record: 35.)
Whew. I haven’t shared this new triangle problem with my coworkers yet. But it’s only a matter of time before they discover it—and argue some more.